Ở phần trước đó, chúng ta đã nêu lên bài toán dữ liệu chuỗi thời gian có 10% data bị NA và sử dụng linear regression để tái tạo các điểm dữ liệu NA trên. Ở bài toán này, chúng ta đi vào luôn phân tích sử dụng Decision Tree Regression thay thế cho liner regression và xem thử việc thay thế nào có mang cho dữ liệu của chúng ta tốt hơn hay không
Ngữ cảnh, chẩn bị dữ liệu giả lập
Mô tả dữ liệu:
- Một chuỗi thời gian từ ngày 1 tháng 1 năm 2025 đến ngày 30 tháng 4 năm 2025 được tạo ra với các khoảng thời gian 10 phút.
- chuỗi thời gian có chu kỳ ngày-đêm: cao vào ban ngày (từ 6 AM đến 6 PM) và thấp vào ban đêm.
Mô tả Dữ Liệu Thiếu:
- 10% giá trị năng lượng được chọn ngẫu nhiên và thay thế bằng
NaNđể mô phỏng dữ liệu bị thiếu.
Code mẫu bằng python
1import pandas as pd
2import numpy as np
3from datetime import datetime
4import matplotlib.pyplot as plt
5
6# Simulate mock energy production dataset
7def simulate_energy_data(start_date, end_date, freq='10min'):
8 # Create a datetime index with 10-minute intervals
9 datetime_index = pd.date_range(start=start_date, end=end_date, freq=freq)
10
11 # Simulate energy production with day-night cycles
12 np.random.seed(42) # For reproducibility
13 hours = datetime_index.hour
14 day_energy = np.random.normal(loc=300, scale=30, size=len(hours))
15 night_energy = np.random.normal(loc=50, scale=15, size=len(hours))
16 energy_values = np.where((hours >= 6) & (hours <= 18), day_energy, night_energy)
17
18 # Introduce missing values (10% of the dataset)
19 num_missing = int(0.1 * len(energy_values)) # 10% of data will be missing
20 missing_indices = np.random.choice(len(energy_values), num_missing, replace=False)
21 energy_values[missing_indices] = np.nan # Set randomly selected indices to NaN
22
23 # Create DataFrame with the simulated energy data
24 energy_data = pd.DataFrame({
25 'Datetime': datetime_index,
26 'Energy_Production': energy_values
27 })
28
29 return energy_data
30
31
32def plot_origin_data(energy_data_with_missing):
33 plt.figure(figsize=(24, 6))
34 plt.plot(energy_data_with_missing['Datetime'], energy_data_with_missing['Energy_Production'], label='Energy Production')
35 plt.xlabel('Datetime')
36 plt.ylabel('Energy Production')
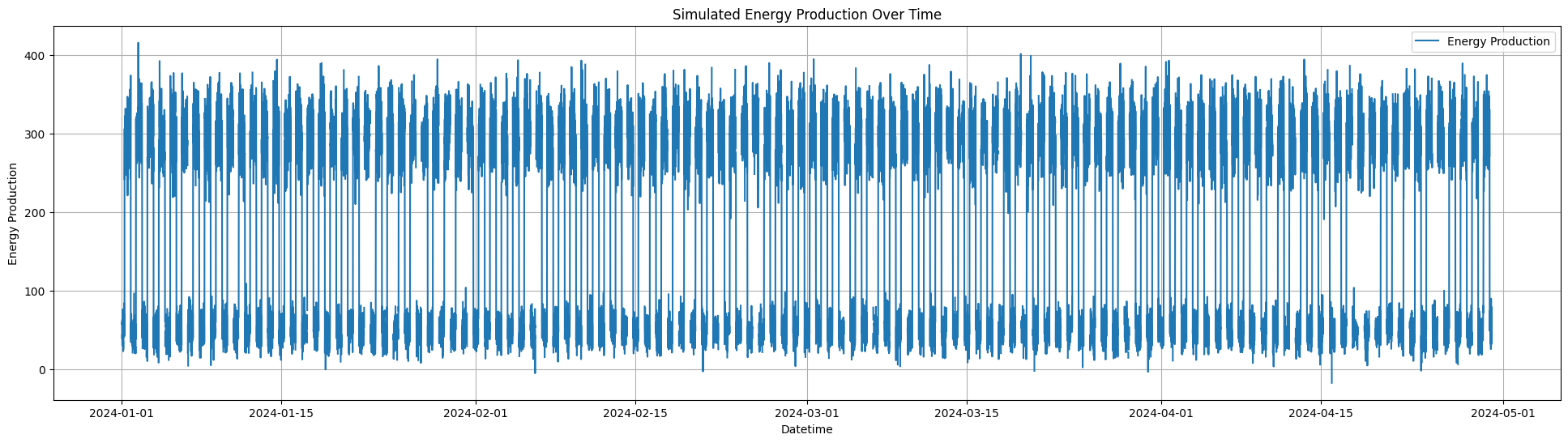
37 plt.title('Simulated Energy Production Over Time')
38 plt.legend()
39
40 plt.grid(True)
41 plt.show()
42# Main script
43if __name__ == "__main__":
44 start_date = datetime(2025, 1, 1)
45 end_date = datetime(2025, 4, 40)
46
47 # Generate the simulated dataset
48 energy_data_with_missing = simulate_energy_data(start_date, end_date)
49
50 # Display the first few rows of the dataset
51 print(energy_data_with_missing.head())
52
53
54 plot_origin_data(energy_data_with_missing)
Phương Pháp tái tạo Dữ Liệu Dựa Trên Decision Tree Regession
1
2from sklearn.tree import DecisionTreeRegressor
3
4# Impute missing values using linear regression
5def impute_missing_values(data):
6 # Extract the non-missing data
7 non_missing_data = data.dropna()
8
9 # Prepare the features (X) and target (y)
10 X = non_missing_data.index.values.reshape(-1, 1)
11 y = non_missing_data['Energy_Production'].values
12
13 # Fit the linear regression model
14 model = DecisionTreeRegressor(max_depth=5, random_state=42)
15 model.fit(X, y)
16
17 # Predict the missing values
18 missing_data = data[data['Energy_Production'].isna()]
19 X_missing = missing_data.index.values.reshape(-1, 1)
20 predicted_values = model.predict(X_missing)
21
22 # Create a DataFrame for the imputed data
23 imputed_data = data.copy()
24 imputed_data.loc[data['Energy_Production'].isna(), 'Energy_Production'] = predicted_values
25
26 return imputed_data
27
28
29def plot_full_data(energy_data_imputed,energy_data_with_missing):
30 plt.figure(figsize=(24, 6))
31
32 plt.plot(energy_data_imputed['Datetime'], energy_data_imputed['Energy_Production'], label='Imputed Data using Decision regression', color='blue' )
33 plt.plot(energy_data_with_missing['Datetime'], energy_data_with_missing['Energy_Production'], label='Original Data', color='red')
34 plt.xlabel('Datetime')
35 plt.ylabel('Energy Production')
36 plt.title('Simulated Energy Production Over Time (Original vs Imputed)')
37 plt.legend()
38 plt.grid(True)
39 plt.show()
40
41# Main script
42if __name__ == "__main__":
43
44 start_date = datetime(2024, 1, 1)
45 end_date = datetime(2024, 4, 30)
46
47 # Generate the simulated dataset
48 energy_data_with_missing = simulate_energy_data(start_date, end_date)
49
50
51 plot_origin_data(energy_data_with_missing)
52
53
54 # Impute the missing values
55 energy_data_imputed = impute_missing_values(energy_data_with_missing.copy())
56
57 # Display the first few rows of the dataset
58 print(energy_data_imputed.head())
59
60 plot_full_data(energy_data_imputed,energy_data_with_missing)
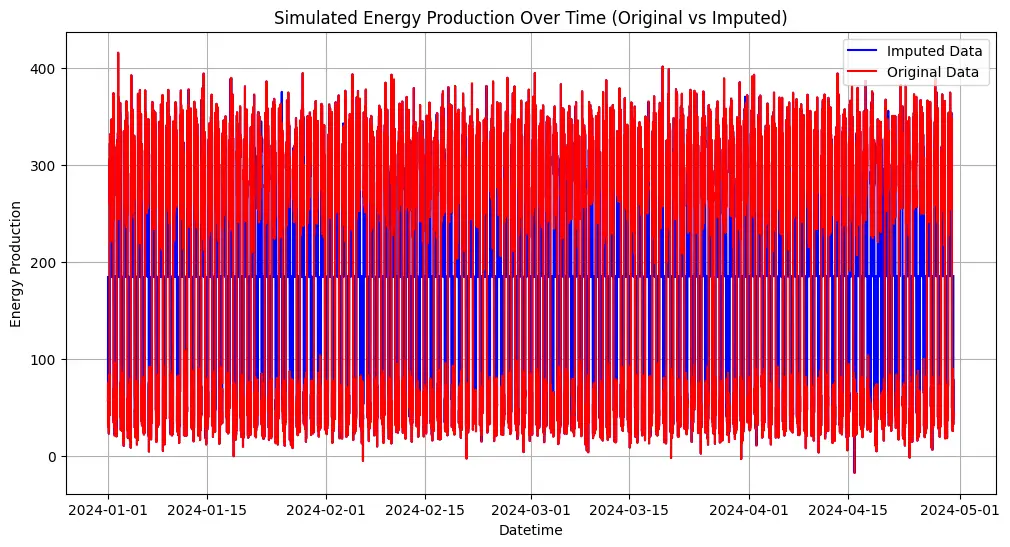
Nhìn đồ thị, chúng ta thấy rằng giá trị của các dữ liệu tái tạo khá tương đồng với dữ liệu gốc. Một số khoảng trống được tái tạo tốt, một số dữ liệu ở điểm cực trị cũng được tái tạo. Cần các phân tích chuyên sâu hơn
Đánh giá hiệu quả của việc tái tạo dữ liệu
1.Statistical Comparison - So sánh thống kê
So sánh các chỉ số thống kê (trung bình, độ lệch chuẩn, giá trị nhỏ nhất, giá trị lớn nhất) để đảm bảo dữ liệu tái tạo phù hợp với phân phối dữ liệu gốc.
1
2# Statistical comparison function using describe
3def statistical_comparison(original_data, imputed_data):
4 original_stats = original_data['Energy_Production'].describe()
5 imputed_stats = imputed_data['Energy_Production'].describe()
6 comparison = pd.DataFrame({
7 'Metric': original_stats.index,
8 'Original Data': original_stats.values,
9 'Imputed Data': imputed_stats.values
10 })
11 return comparison
12
13comparison = statistical_comparison(energy_data_with_missing.dropna(), energy_data_imputed)
14print(comparison)
Kết quả
1 Metric Original Data Imputed Data
20 count 15553.000000 17281.000000
31 mean 185.155737 185.170568
42 std 127.062030 120.682665
53 min -16.984058 -16.984058
64 25% 51.260972 53.345570
75 50% 257.313693 185.457881
86 75% 302.393653 298.754461
97 max 415.581945 415.581945
So sánh với Linear Regression ở bài trước đó
1 Metric Original Data Imputed Data Linear Regression
20 count 15553.000000 17281.000000
31 mean 185.155737 185.155865
42 std 127.062030 120.541640
53 min -16.984058 -16.984058
64 25% 51.260972 53.436820
75 50% 257.313693 185.404682
86 75% 302.393653 298.653209
97 max 415.581945 415.581945
Từ bảng so sánh thống kê ở trên , chúng ta có thể rút ra những kết luận sau:
Số Lượng (Count): Bộ dữ liệu tái tạo chứa nhiều điểm dữ liệu hơn, 17281, so với bộ dữ liệu gốc, 15553, do việc tái tạo các giá trị thiếu để đảm bảo dữ liệu đầy đủ.
Trung Bình (Mean): Trung bình của dữ liệu tái tạo là 185.17, gần giống với giá trị trung bình của dữ liệu gốc 185.15, điều này có nghĩa là xu hướng trung tâm của dữ liệu đã được duy trì trong quá trình tái tạo dữ liệu. Tuy nhiên, Linear Regression cho giá trị trung bình gần với tập dữ liệu gốc hơn.
Độ Lệch Chuẩn (Standard Deviation): Dữ liệu tái tạo có sự phân tán thấp hơn (độ lệch chuẩn = 120.6 so với 127.06 của dữ liệu gốc). Điều này có thể cho thấy rằng trong quá trình tái tạo dữ liệu, các giá trị đã trở nên mượt mà hơn, giảm bớt sự phân tán
Giá Trị Tối Thiểu và Tối Đa: Giá trị tối thiểu (-16.984058) và tối đa (415.581945) là giống nhau, điều này gợi ý rằng quá trình tái tạo dữ liệu không tạo ra các giá trị ngoại lai cực đoan hoặc không đi ra ngoài phạm vi của dữ liệu gốc.
Các Phân Vị (Quartiles 25%, 50%, 75%):
-
Phân vị thứ 25 (quartile thấp) cao hơn một chút trong dữ liệu tái tạo , 53.345570 so với 51.26 của dữ liệu gốc, cho thấy các giá trị tái tạo đã lấp đầy nhiều khoảng trống ở phạm vi thấp.
-
Trung vị (50%) đã thay đổi đáng kể từ 257.31 trong dữ liệu gốc thành 185.45 trong dữ liệu tái tạo , cho thấy các giá trị tái tạo đã giảm độ lệch dữ liệu của các phần tử dữ liệu cao.
-
Phân vị thứ 75 (quartile cao) 302.39 và 298.75 , gần như tương đương nhau, phản ánh rằng các giá trị cao đã được bảo tồn tốt.
Kết luận: Phương pháp hồi quy Decision Tree đã bảo tồn phân phối tổng thể và phạm vi của dữ liệu, trong khi làm giảm sự biến thiên và làm mượt dữ liệu một chút.
2.Autocorrelation
Kiểm tra xem tự tương quan của chuỗi có được duy trì sau khi tái tạo dữ liệu hay không.
1
2
3# Autocorrelation analysis function
4def autocorrelation_analysis(original_data, imputed_data):
5 fig, axes = plt.subplots(1, 2, figsize=(15, 6))
6 plot_acf(original_data['Energy_Production'].dropna(), ax=axes[0], title='ACF of Original Data')
7 plot_acf(imputed_data['Energy_Production'], ax=axes[1], title='ACF of Imputed Data')
8 plt.tight_layout()
9 plt.show()
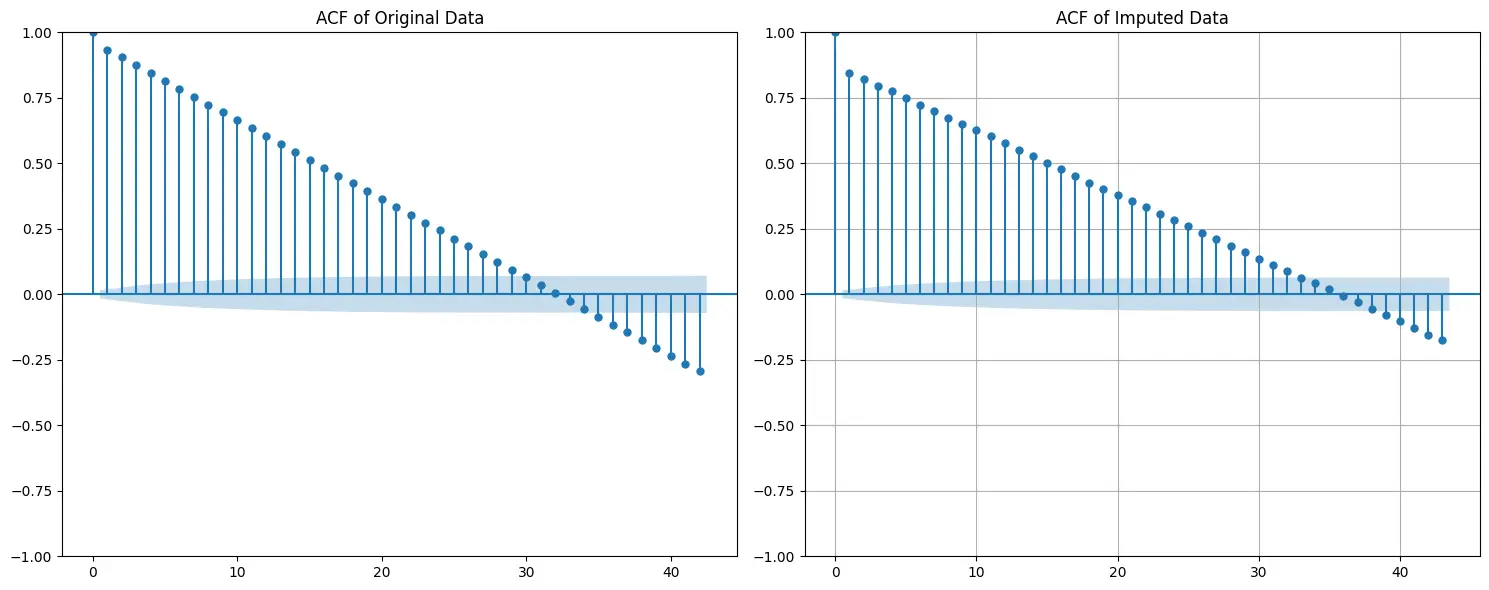
Quan sát đồ thị ACF trên, chúng ta có thể rút ra các ý chính sau
Bảo Tồn Các Phụ Thuộc - Preservation of Temporal Dependencies:
Hình dạng và sự suy giảm của ACF trong dữ liệu tái tạo có sự tương đồng đáng kể với dữ liệu gốc. Điều này cho thấy rằng các phụ thuộc thời gian đã được bảo tồn khá tốt sau quá trình tái tạo dữ liệu.
Hiệu Ứng Làm Mịn - Slight Smoothing Effect:
ACF trên dữ liệu tái tạo cho thấy giá trị ở một số độ trễ (lags) thấp hơn so với dữ liệu gốc. Điều này có thể là do mô hình hồi quy tuyến tính làm mịn các cực trị, dẫn đến giảm nhẹ mức độ biến động.
Các Mẫu Chu Kỳ Trong ACF - Cyclic Patterns:
Các đỉnh chu kỳ trong ACF, chẳng hạn như tính mùa vụ hàng ngày, dường như được duy trì giữa dữ liệu gốc và dữ liệu tái tạo . Điều này cho thấy rằng quá trình tái tạo dữ liệu đã bảo tồn các hành vi tuần hoàn trong tập dữ liệu.
Tính Ổn Định Chung:
Sự tương đồng giữa hai biểu đồ ACF là một dấu hiệu tích cực, cho thấy phương pháp tái tạo dữ liệu bằng hồi quy tuyến tính đã giữ lại tốt cấu trúc cốt lõi trong dữ liệu.
Kết Luận:
Phương pháp hồi quy tuyến tính không chỉ bảo tồn mối liên hệ thời gian trong dữ liệu mà còn duy trì các mẫu chu kỳ, mặc dù có một chút hiệu ứng làm mịn.
3. Phân tích xu hướng và mùa vụ - STL Decomposition (Trend and Seasonality)
So Sánh Xu Hướng (Trend Comparison)
1
2# STL decomposition function to extract and plot trend component
3def stl_decomposition_trend(original_data, imputed_data, period):
4 stl_original = STL(original_data['Energy_Production'] , period=period)
5 result_original = stl_original.fit()
6 trend_original = result_original.trend
7
8 stl_imputed = STL(imputed_data['Energy_Production'], period=period)
9 result_imputed = stl_imputed.fit()
10 trend_imputed = result_imputed.trend
11
12 plt.figure(figsize=(24, 6))
13 plt.plot(original_data['Datetime'], trend_original, label='Trend of Original Data', color='red')
14 plt.plot(imputed_data['Datetime'], trend_imputed, label='Trend of Imputed Data', color='blue')
15 plt.xlabel('Datetime')
16 plt.ylabel('Trend')
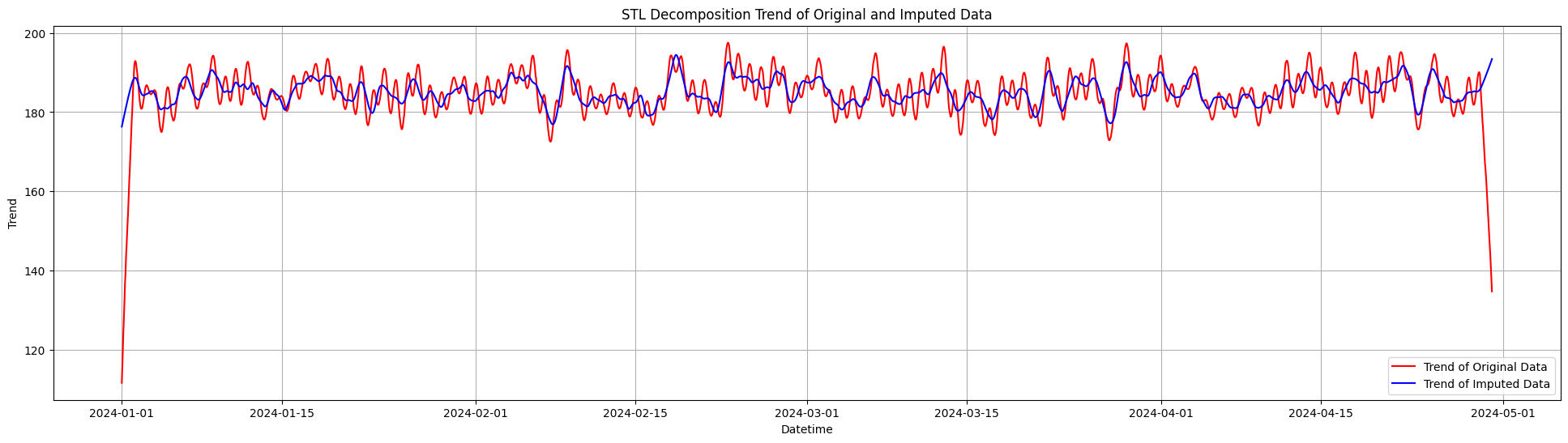
17 plt.title('STL Decomposition Trend of Original and Imputed Data')
18 plt.legend()
19 plt.grid(True)
20 plt.show()
21
22stl_decomposition_trend(energy_data_with_missing.dropna(), energy_data_imputed, period=144) # Daily seasonality (144 10-min intervals in a day)
-
Bảo Tồn Xu Hướng Dài Hạn:
Đường Xu hướng tái tạo (màu xanh dương) nhìn chung phù hợp với xu hướng gốc (màu đỏ), cho thấy phương pháp tái tạo hồi quy tuyến tính đã bảo tồn được chuyển động dài hạn trong dữ liệu.
-
Hiệu Ứng Làm Mịn:
Đường Xu hướng tái tạo mượt mà hơn so với xu hướng gốc, đặc biệt ở những nơi xu hướng gốc có nhiều biến động. Điều này là đặc điểm của hồi quy tuyến tính, vốn có xu hướng không phản ánh tốt các biến động mạnh và làm mịn các cực trị.
So Sánh Tính Mùa Vụ (Seasonality Comparison)
1
2
3def stl_decomposition_seasonality(original_data, imputed_data, period):
4 stl_original = STL(original_data['Energy_Production'], period=period)
5 result_original = stl_original.fit()
6 seasonality_original = result_original.seasonal
7
8 stl_imputed = STL(imputed_data['Energy_Production'], period=period)
9 result_imputed = stl_imputed.fit()
10 seasonality_imputed = result_imputed.seasonal
11
12 plt.figure(figsize=(24, 6))
13 plt.plot(original_data['Datetime'], seasonality_original, label='Seasonality of Original Data', color='red')
14 plt.plot(imputed_data['Datetime'], seasonality_imputed, label='Seasonality of Imputed Data', color='blue')
15 plt.xlabel('Datetime')
16 plt.ylabel('Seasonality')
17 plt.title('STL Decomposition Seasonality of Original and Imputed Data')
18 plt.legend()
19 plt.grid(True)
20 plt.show()
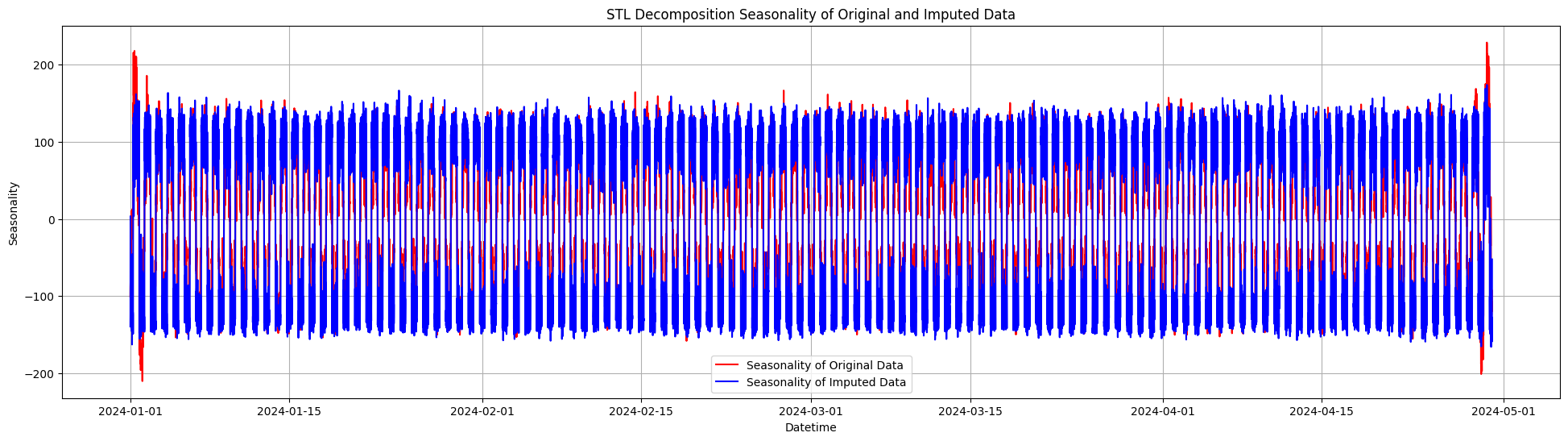
21stl_decomposition_seasonality(energy_data_with_missing.dropna(), energy_data_imputed, period=144) # Daily seasonality (144 10-min intervals in a day)
-
Bảo Tồn tính Chu Kỳ:
Đường mùa vụ tái tạo thể hiện ra các mẫu chu kỳ tương đối gần giống với chu kỳ của đường mùa vụ gốc, phản ánh rằng dữ liệu các chu kỳ sản xuất ngày-đêm đã được duy trì khá tốt.
-
Giảm Biên Độ Chu Kỳ:
Biên độ của đường mùa vụ tái tạo bị giảm nhẹ so với gốc, đặc biệt tại các đỉnh và đáy. Điều này cho thấy quá trình tái tạo dữ liệu đã làm cho các biến động chu kỳ ở cực trị trở nên ít mạnh mẽ hơn.
Hạn Chế Của tái tạo Dữ Liệu Bằng Hồi Quy Tuyến Tính
Làm Mịn Các cực trị:
-
Từ so sánh thống kê, độ lệch chuẩn thấp hơn ở dữ liệu tái tạo cho thấy tính biến động đã bị giảm.
-
Từ so sánh xu hướng, xu hướng tái tạo mượt hơn và thiếu một số biến động gốc trong các mẫu dài hạn.
Giả Định Tuyến Tính:
- Hiệu ứng làm mịn trong so sánh xu hướng cho thấy phương pháp này khó bắt kịp các thay đổi phi tuyến tính trong dữ liệu, đặc biệt tại các giai đoạn có sự thay đổi đột ngột.
Giảm Biên Độ Mùa Vụ:
- So sánh tính mùa vụ cho thấy biên độ chu kỳ tái tạo thấp hơn so với gốc, với các đỉnh và đáy bị làm mịn. Điều này phù hợp với xu hướng của hồi quy trong việc kéo các giá trị cực đoan về trung bình.
Kết luận
Phương pháp tái tạo hồi quy tuyến tính bảo tồn được các xu hướng tổng thể và các mẫu chu kỳ, nhưng làm giảm tính biến động và làm mịn các giá trị cực đoan. Ngoài ra, nó thể hiện sự giảm nhẹ cường độ của các chu kỳ mùa vụ, điều này được phản ánh trong cả phân tích thống kê và phân rã dữ liệu.
Trong bài toán này, sự khác biệt của Decision Tree và linear regression không rõ ràng lắm, cả hai đều đáp ứng tốt nhu cầu tái tạo dữ liệu.
Cảm ơn các bạn đã theo dõi bài viết. Xin cảm ơn và hẹn gặp lại.
Tài liệu tham khảo
https://www.geeksforgeeks.org/managing-missing-data-in-linear-regression/
https://towardsdatascience.com/missing-data-in-time-series-machine-learning-techniques-6b2273ff8b45
https://www.geeksforgeeks.org/dataset-for-linear-regression/
https://www.geeksforgeeks.org/ml-handling-missing-values/
https://codezup.com/mastering-linear-regression-time-series-forecasting/
Comments